本文python代码均为在Jupyter Lab上完成，可在Github上查看：data-ming-summary

分类、回归、聚类概念辨析

  1. 分类（Classification）
    eg：性别预测
    👉有监督学习（数据有标记，并且是类别型数据）
    通过数据矩阵X和数据对应的标记（label）Y构建模型，可以对未知label的数据X'进行分类预测，得出Y'
  2. 回归（Regression）
    eg：身高⇨体重
    和分类类似，但标记Y是数值型数据
  3. 聚类（Clustering）
    👉无监督学习（数据无标记）
    对数据进行特征提取，分成几个类别，但并不知道类别是什么
  4. 降维（Dimension Reduction）
    👉无监督学习
    由数据矩阵X到X'，提取主要信息，降低数据维度，如PCA主成分分析

支持向量机

首先，直观的感受下什么是支持向量机：


因为还没有完全理解、证明SVM算法，我只能先推荐一些教程。

推荐视频教程学习：【机器学习】【白板推导系列】【合集 1～33】

推荐文章教程学习：机器学习实战教程（八）：支持向量机原理篇之手撕线性SVM

一个代码例子：

lsvm_clf = LinearSVC(dual=False, random_state=0)  # 样本量大于特征数，将对偶项设为False
%time lsvm_clf.fit(x_train, y_train)   # 拟合训练集

lsvm_pred = lsvm_clf.predict(x_test)  # 预测测试集
lsvm_prob = lsvm_clf._predict_proba_lr(x_test)  # 测试集类别的概率

lsvm_fpr, lsvm_tpr, _ = roc_curve(y_test, lsvm_prob[:, 1])  # 得到真假阳性率数据
lsvm_area = round(roc_auc_score(y_test, lsvm_prob[:, 1]), 3)  # AUC值，保留3为小数
lsvm_precision, lsvm_recall, _ = precision_recall_curve(y_test, lsvm_prob[:, 1])  # 准确率与回归率
lsvm_pr_auc = round(auc(lsvm_recall, lsvm_precision), 3)

lsvm_Accuracy = round(lsvm_clf.score(x_test, y_test), 3)  # 模型精度
lsvm_Precision = round(precision_score(y_test, lsvm_pred), 3)
lsvm_Recall = round(recall_score(y_test, lsvm_pred), 3)
lsvm_F1_score = round(f1_score(y_test, lsvm_pred), 3)

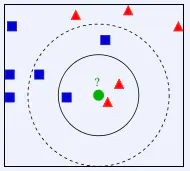
K-最近邻（KNN）

  1. 算法介绍：

    有一个已知的样本数据集（训练集），包含其对应的标签，输入无标签的测试数据集，要求其对应的标签，可以计算每个测试样本与训练集的每个样本的距离，然后取最近的K个训练集样本标签，把这K个样本中标签较多的一类作为当前待求测试样本的标签。
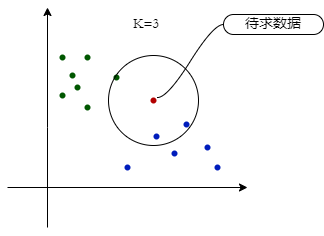
    KNN原理

    以上是我通俗的表述，用算法的形式表示出来如下：

    令K是最近邻数目，D是训练样本的集合
for 每个测试样本z=(x',y'):
    计算z和每个训练样本(x,y)∈D的距离d(x,x');
    选择和z最近的K个训练样本集合D₀∈D;
    投票表决（多数表决或距离加权表决）
end

    其中，计算样本的距离需要根据具体情况选择合适的方法。

    ①欧氏距离

    经常使用的一种距离，通常要进行归一化处理

    ②余弦相似度

    不考虑向量的大小，只关注方向

    ③曼哈顿距离

    ④切比雪夫距离

    两个向量在任意坐标维度上的最大差值

    ⑤闵可夫斯基距离

    其中：

    • p=1：曼哈顿距离
    • p=2：欧氏距离
    • p=∞：且比雪夫距离

    参考：

    1. 数据科学中常见的9种距离度量方法，内含欧氏距离、切比雪夫距离等 - 知乎 (zhihu.com)

    2. Python Numpy计算各类距离的方法_方法_Python_NumPy - 1024问 (mscto.com)

  2. python手动实现

    # In[1]:
# 导入包
import os
import numpy as np
from sklearn.neighbors import KNeighborsClassifier as KNC

from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"  # 设置多输出


# In[2]:
# 设定数据集路径
test_path = 'dataset/testDigits'
train_path = 'dataset/trainingDigits'


# In[16]:
# 读取和处理数据
test_files = os.listdir(test_path)  # 列出数据集所有文件
train_files = os.listdir(train_path)
test_x = []
test_y = []
train_x = []
train_y = []

for tf in test_files:
    with open(os.path.join(test_path, tf), 'r') as fp:
        t = fp.read()  # 读取文件
        t = t.replace('\n', '')
        t = np.array(list(t)).astype(int)  # 转换为int类型
        test_x.append(t)
        t_label = int(tf.split('_')[0])  # 获取数据的标签
        test_y.append(t_label)
test_y = np.array(test_y)

for tf in train_files:
    with open(os.path.join(train_path, tf), 'r') as fp:
        t = fp.read()
        t = t.replace('\n', '')
        t = np.array(list(t)).astype(int)
        train_x.append(t)
        t_label = int(tf.split('_')[0])
        train_y.append(t_label)
train_y = np.array(train_y)


# In[17]:
# 实现KNN算法核心原理
def get_distance(X, Y, method='euclidean'):
    """
    计算向量X、Y的各种距离，X与Y均为np.array数组，method为字符串，表示计算哪种距离
    """
    if method == 'euclidean':  # 欧氏距离
        return np.linalg.norm(X - Y)
    elif method == 'cosine':  # 余弦相似度
        return np.dot(X, Y)/(np.linalg.norm(X) * np.linalg.norm(Y))
    elif method == 'manhattan':  # 曼哈顿距离
        return np.sum(np.abs(X - Y))
    elif method == 'chebyshev':  # 切比雪夫距离
        return np.abs(X - Y).max()
    else:
        raise ValueError('没有此距离参数')


def knn_algorithm(test_X, train_X, train_Y, distance='euclidean', k: int=3):
    """
    输入测试数据集、训练数据集及其标签，distance为计算距离的方式，与get_distance函数里的method参数一样，k为选取最小距离样本的个数
    """
    test_Y = []  # 待求测试数据集的标签
    for tX in test_X:  # 循环测试样本
        td  = []  # 中间变量，当前测试样本与训练集的距离数组
        for rX in train_X:
            td.append(get_distance(tX, rX, method=distance))  # 计算距离后加到td中间变量
        idx = np.argpartition(np.array(td), k)[:k]  # 找出距离最小的k个样本的位置序号
        ty = train_Y[idx]  # k个训练集样本的标签
        test_Y.append(np.argmax(np.bincount(ty)))  # 统计这k个训练集样本的标签，多数表决，添加到test_Y末尾
    return test_Y


# In[18]:
# 调用knn算法，求测试数据集的标签
predict_y1 = np.array(knn_algorithm(test_x, train_x, train_y))


# In[19]:
# 计算准确率
accuracy1 = np.mean(np.equal(predict_y1, test_y))  # 计算分类的准确度
'准确率', accuracy1
err_label_idx1 = np.where(np.equal(predict_y1, test_y) == False)[0]  # 错误分类的位置序号
err_label_num1 = len(err_label_idx1)  # 错误分类的个数
'错误分类个数', err_label_num1
err_label1 = test_y[err_label_idx1]  # 错误分类的正确标签
err_pred_label1 = predict_y1[err_label_idx1]  # 预测的标签
'正确标签', err_label1, '预测的标签', err_pred_label1


# In[20]:
# 再使用sklearn的KNN分类器构建和上面一样的分类器，进行分类
clf = KNC(n_neighbors=3)  # 构建的分类器，设定K为3
clf.fit(train_x, train_y)  # 拟合


# In[21]:
# 预测测试集的标签
predict_y2 = clf.predict(test_x)


# In[22]:
# 计算分类器的平均准确率
accuracy2 = clf.score(test_x, test_y)
'准确率', accuracy2
err_label_idx2 = np.where(np.equal(predict_y2, test_y) == False)[0]  # 错误分类的位置序号
err_label_num2 = len(err_label_idx2)  # 错误分类的个数
'错误分类个数', err_label_num2
err_label2 = test_y[err_label_idx2]  # 错误分类的正确标签
err_pred_label2 = predict_y2[err_label_idx2]  # 预测的标签
'正确标签', err_label2, '预测的标签', err_pred_label2
    knn_algorithm KNeighborsClassifier
    准确率 98.84 98.73
    误分类个数 11 12

    虽然手写的算法代码准确率高了一点点，但是分类时间却远大于sklearn的分类器。

  3. KNN优缺点
    ⑴优点：

    • 算法简单，易实现，精度高
    • 可用于数值型和离散型数据，换句话说就是可以用于回归和分类
    • 分类时间复杂度为O(n)

      这里的时间复杂度应该是求一个样本的时间。设测试集样本量为n，训练集样本量为m，那么整体时间复杂度应该是O(m*n)

    ⑵缺点：

    • 计算复杂性高；空间复杂性高
    • 对噪声敏感
    • 样本不平衡问题
      即有些类别的样本数量很多，而其它样本的数量很少，使用一般的多数表决就不准确，解决方法是使用距离加权表决，越近的加权越大。
      样本不平衡
    • 较难找到最优的K值
      找到合适的K值对分类准确率有影响，一般都是用试探法来确定K值。
      较难确定K值